Решение систем линейных алгебраических уравнений, методы решения, примеры. Системы линейных уравнений

Система линейных уравнений - это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

Решение системы уравнений - это последовательность чисел (k 1 , k 2 , ..., k n ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x 1 , x 2 , ..., x n дает верное числовое равенство.

Соответственно, решить систему уравнений - значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» - надо описать, как устроено это множество.

Переменная x i называется разрешенной, если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной x i должен быть равен нулю.

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x 1 , x 3 и x 4 . Впрочем, с тем же успехом можно утверждать, что вторая система - разрешенная относительно x 1 , x 3 и x 5 . Достаточно переписать самое последнее уравнение в виде x 5 = x 4 .

Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:

Число разрешенных переменных r равно общему числу переменных k : r = k . Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x 1 = b 1 , x 2 = b 2 , ..., x k = b k ;
Число разрешенных переменных r меньше общего числа переменных k : r < k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Так, в приведенных выше системах переменные x 2 , x 5 , x 6 (для первой системы) и x 2 , x 5 (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:

Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.

Теорема. Если в системе из n уравнений переменные x 1 , x 2 , ..., x r - разрешенные, а x r + 1 , x r + 2 , ..., x k - свободные, то:

Если задать значения свободным переменным (x r + 1 = t r + 1 , x r + 2 = t r + 2 , ..., x k = t k ), а затем найти значения x 1 , x 2 , ..., x r , получим одно из решений.

Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.

В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все - таким образом можно получить все решения системы. Других решений не существует.

Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше - неопределенной.

И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует

где x * - один из решений неоднородной системы (2) (например (4)), (E−A + A) образует ядро (нуль пространство) матрицы A .

Сделаем скелетное разложение матрицы (E−A + A) :

E−A + A=Q·S

где Q n×n−r - матрица rank(Q)=n−r , S n−r×n -матрица rank(S)=n−r .

Тогда (13) можно записать в следующем виде:

x=x*+Q·k, ∀ k∈ R n-r .

где k=Sz .

Итак, процедура нахождения общего решения системы линейных уравнений с помощью псевдообратной матрицы можно представить в следующем виде:

Вычисляем псевдообратную матрицу A + .
Вычисляем частное решение неоднородной системы линейных уравнений (2): x *=A + b .
Проверяем совместность системы. Для этого вычисляем AA + b . Если AA + b ≠b , то система несовместна. В противном случае продолжаем процедуру.
Высисляем E−A + A.
Делаем скелетное разложение E−A + A=Q·S.
Строим решение

x=x*+Q·k, ∀ k∈ R n-r .

Решение системы линейных уравнений онлайн

Онлайн калькулятор позволяет найти обшее решение системы линейных уравнений с подробными объяснениями.

Высшая математика » Системы линейных алгебраических уравнений » Основные термины. Матричная форма записи.

Система линейных алгебраических уравнений. Основные термины. Матричная форма записи.

Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.
Матричная форма записи систем линейных алгебраических уравнений.

Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.

Под системой линейных алгебраических уравнений (СЛАУ) подразумевают систему

\begin{equation} \left \{ \begin{aligned} & a_{11}x_1+a_{12}x_2+a_{13}x_3+\ldots+a_{1n}x_n=b_1;\\ & a_{21}x_1+a_{22}x_2+a_{23}x_3+\ldots+a_{2n}x_n=b_2;\\ & \ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots \\ & a_{m1}x_1+a_{m2}x_2+a_{m3}x_3+\ldots+a_{mn}x_n=b_m. \end{aligned} \right. \end{equation}

Параметры $a_{ij}$ ($i=\overline{1,m}$, $j=\overline{1,n}$) называют коэффициентами , а $b_i$ ($i=\overline{1,m}$) - свободными членами СЛАУ. Иногда, чтобы подчеркнуть количество уравнений и неизвестных, говорят так «$m\times n$ система линейных уравнений», - тем самым указывая, что СЛАУ содержит $m$ уравнений и $n$ неизвестных.

Если все свободные члены $b_i=0$ ($i=\overline{1,m}$), то СЛАУ называют однородной . Если среди свободных членов есть хотя бы один, отличный от нуля, СЛАУ называют неоднородной .

Решением СЛАУ (1) называют всякую упорядоченную совокупность чисел ($\alpha_1, \alpha_2,\ldots,\alpha_n$), если элементы этой совокупности, подставленные в заданном порядке вместо неизвестных $x_1,x_2,\ldots,x_n$, обращают каждое уравнение СЛАУ в тождество.

Любая однородная СЛАУ имеет хотя бы одно решение: нулевое (в иной терминологии - тривиальное), т.е. $x_1=x_2=\ldots=x_n=0$.

Если СЛАУ (1) имеет хотя бы одно решение, ее называют совместной , если же решений нет - несовместной . Если совместная СЛАУ имеет ровно одно решение, её именуют определённой , если бесконечное множество решений - неопределённой .

Пример №1

Рассмотрим СЛАУ

\begin{equation} \left \{ \begin{aligned} & 3x_1-4x_2+x_3+7x_4-x_5=11;\\ & 2x_1+10x_4-3x_5=-65;\\ & 3x_2+19x_3+8x_4-6x_5=0. \\ \end {aligned} \right. \end{equation}

Имеем систему линейных алгебраических уравнений, содержащую $3$ уравнения и $5$ неизвестных: $x_1,x_2,x_3,x_4,x_5$. Можно, сказать, что задана система $3\times 5$ линейных уравнений.

Коэффициентами системы (2) есть числа, стоящие перед неизвестными. Например, в первом уравнении эти числа таковы: $3,-4,1,7,-1$. Свободные члены системы представлены числами $11,-65,0$. Так как среди свободных членов есть хотя бы один, не равный нулю, то СЛАУ (2) является неоднородной.

Упорядоченная совокупность $(4;-11;5;-7;1)$ является решением данной СЛАУ. В этом несложно убедиться, если подставить $x_1=4; x_2=-11; x_3=5; x_4=-7; x_5=1$ в уравнения заданной системы:

\begin{aligned} & 3x_1-4x_2+x_3+7x_4-x_5=3\cdot4-4\cdot(-11)+5+7\cdot(-7)-1=11;\\ & 2x_1+10x_4-3x_5=2\cdot 4+10\cdot (-7)-3\cdot 1=-65;\\ & 3x_2+19x_3+8x_4-6x_5=3\cdot (-11)+19\cdot 5+8\cdot (-7)-6\cdot 1=0. \\ \end{aligned}

Естественно, возникает вопрос том, является ли проверенное решение единственным. Вопрос о количестве решений СЛАУ будет затронут в соответствующей теме.

Пример №2

Рассмотрим СЛАУ

\begin{equation} \left \{ \begin{aligned} & 4x_1+2x_2-x_3=0;\\ & 10x_1-x_2=0;\\ & 5x_2+4x_3=0; \\ & 3x_1-x_3=0;\\ & 14x_1+25x_2+5x_3=0. \end{aligned} \right. \end{equation}

Система (3) является СЛАУ, содержащей $5$ уравнений и $3$ неизвестных: $x_1,x_2,x_3$. Так как все свободные члены данной системы равны нулю, то СЛАУ (3) является однородной. Несложно проверить, что совокупность $(0;0;0)$ является решением данной СЛАУ. Подставляя $x_1=0, x_2=0,x_3=0$, например, в первое уравнение системы (3), получим верное равенство: $4x_1+2x_2-x_3=4\cdot 0+2\cdot 0-0=0$. Подстановка в иные уравнения делается аналогично.

Матричная форма записи систем линейных алгебраических уравнений.

С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:

Матрица $A$ называется матрицей системы . Элементы данной матрицы представляют собой коэффициенты заданной СЛАУ.

Матрица $\widetilde{A}$ называется расширенной матрицей системы . Её получают добавлением к матрице системы столбца, содержащего свободные члены $b_1,b_2,…,b_m$. Обычно этот столбец отделяют вертикальной чертой, - для наглядности.

Матрица-столбец $B$ называется матрицей свободных членов , а матрица-столбец $X$ - матрицей неизвестных .

Используя введённые выше обозначения, СЛАУ (1) можно записать в форме матричного уравнения: $A\cdot X=B$.

Примечание

Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков (см. пример №4).

Пример №3

Записать СЛАУ $ \left \{ \begin{aligned} & 2x_1+3x_2-5x_3+x_4=-5;\\ & 4x_1-x_3=0;\\ & 14x_2+8x_3+x_4=-11. \end{aligned} \right. $ в матричной форме и указать расширенную матрицу системы.

Имеем четыре неизвестных, которые в каждом уравнении следуют в таком порядке: $x_1,x_2,x_3,x_4$. Матрица неизвестных будет такой: $\left(\begin{array} {c} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right)$.

Свободные члены данной системы выражены числами $-5,0,-11$, посему матрица свободных членов имеет вид: $B=\left(\begin{array} {c} -5 \\ 0 \\ -11 \end{array} \right)$.

Перейдем к составлению матрицы системы. В первую строку данной матрицы будут занесены коэффициенты первого уравнения: $2,3,-5,1$.

Во вторую строку запишем коэффициенты второго уравнения: $4,0,-1,0$. При этом следует учесть, что коэффициенты системы при переменных $x_2$ и $x_4$ во втором уравнении равны нулю (ибо эти переменные во втором уравнении отсутствуют).

В третью строку матрицы системы запишем коэффициенты третьего уравнения: $0,14,8,1$. Учитываем при этом равенство нулю коэффициента при переменной $x_1$(эта переменная отсутствует в третьем уравнении). Матрица системы будет иметь вид:

$$ A=\left(\begin{array} {cccc} 2 & 3 & -5 & 1\\ 4 & 0 & -1 & 0 \\ 0 & 14 & 8 & 1 \end{array} \right) $$

Чтобы была нагляднее взаимосвязь между матрицей системы и самой системой, я запишу рядом заданную СЛАУ и ее матрицу системы:

В матричной форме заданная СЛАУ будет иметь вид $A\cdot X=B$. В развернутой записи:

$$ \left(\begin{array} {cccc} 2 & 3 & -5 & 1\\ 4 & 0 & -1 & 0 \\ 0 & 14 & 8 & 1 \end{array} \right) \cdot \left(\begin{array} {c} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right) = \left(\begin{array} {c} -5 \\ 0 \\ -11 \end{array} \right) $$

Запишем расширенную матрицу системы. Для этого к матрице системы $ A=\left(\begin{array} {cccc} 2 & 3 & -5 & 1\\ 4 & 0 & -1 & 0 \\ 0 & 14 & 8 & 1 \end{array} \right) $ допишем столбец свободных членов (т.е. $-5,0,-11$). Получим: $\widetilde{A}=\left(\begin{array} {cccc|c} 2 & 3 & -5 & 1 & -5 \\ 4 & 0 & -1 & 0 & 0\\ 0 & 14 & 8 & 1 & -11 \end{array} \right) $.

Пример №4

Записать СЛАУ $ \left \{\begin{aligned} & 3y+4a=17;\\ & 2a+4y+7c=10;\\ & 8c+5y-9a=25; \\ & 5a-c=-4. \end{aligned}\right.$ в матричной форме и указать расширенную матрицу системы.

Как видите, порядок следования неизвестных в уравнениях данной СЛАУ различен. Например, во втором уравнении порядок таков: $a,y,c$, однако в третьем уравнении: $c,y,a$. Перед тем, как записывать СЛАУ в матричной форме, порядок следования переменных во всех уравнениях нужно сделать одинаковым.

Упорядочить переменные в уравнениях заданной СЛАУ можно разными способами (количество способов расставить три переменные составит $3!=6$). Я разберу два способа упорядочивания неизвестных.

Способ №1

Введём такой порядок: $c,y,a$. Перепишем систему, расставляя неизвестные в необходимом порядке: $\left \{\begin{aligned} & 3y+4a=17;\\ & 7c+4y+2a=10;\\ & 8c+5y-9a=25; \\ & -c+5a=-4. \end{aligned}\right.$

Для наглядности я запишу СЛАУ в таком виде: $\left \{\begin{aligned} & 0\cdot c+3\cdot y+4\cdot a=17;\\ & 7\cdot c+4\cdot y+2\cdot a=10;\\ & 8\cdot c+5\cdot y-9\cdot a=25; \\ & -1\cdot c+0\cdot y+5\cdot a=-4. \end{aligned}\right.$

Матрица системы имеет вид: $ A=\left(\begin{array} {ccc} 0 & 3 & 4 \\ 7 & 4 & 2\\ 8 & 5 & -9 \\ -1 & 0 & 5 \end{array} \right) $. Матрица свободных членов: $B=\left(\begin{array} {c} 17 \\ 10 \\ 25 \\ -4 \end{array} \right)$. При записи матрицы неизвестных помним о порядке следования неизвестных: $X=\left(\begin{array} {c} c \\ y \\ a \end{array} \right)$. Итак, матричная форма записи заданной СЛАУ такова: $A\cdot X=B$. В развёрнутом виде:

$$ \left(\begin{array} {ccc} 0 & 3 & 4 \\ 7 & 4 & 2\\ 8 & 5 & -9 \\ -1 & 0 & 5 \end{array} \right) \cdot \left(\begin{array} {c} c \\ y \\ a \end{array} \right) = \left(\begin{array} {c} 17 \\ 10 \\ 25 \\ -4 \end{array} \right) $$

Расширенная матрица системы такова: $\left(\begin{array} {ccc|c} 0 & 3 & 4 & 17 \\ 7 & 4 & 2 & 10\\ 8 & 5 & -9 & 25 \\ -1 & 0 & 5 & -4 \end{array} \right) $.

Способ №2

Введём такой порядок: $a,c,y$. Перепишем систему, расставляя неизвестные в необходимом порядке: $\left \{ \begin{aligned} & 4a+3y=17;\\ & 2a+7c+4y=10;\\ & -9a+8c+5y=25; \\ & 5a-c=-4. \end{aligned}\right.$

Для наглядности я запишу СЛАУ в таком виде: $\left \{ \begin{aligned} & 4\cdot a+0\cdot c+3\cdot y=17;\\ & 2\cdot a+7\cdot c+4\cdot y=10;\\ & -9\cdot a+8\cdot c+5\cdot y=25; \\ & 5\cdot c-1\cdot c+0\cdot y=-4. \end{aligned}\right.$

Матрица системы имеет вид: $ A=\left(\begin{array} {ccc} 4 & 0 & 3 \\ 2 & 7 & 4\\ -9 & 8 & 5 \\ 5 & -1 & 0 \end{array} \right)$. Матрица свободных членов: $B=\left(\begin{array} {c} 17 \\ 10 \\ 25 \\ -4 \end{array} \right)$. При записи матрицы неизвестных помним о порядке следования неизвестных: $X=\left(\begin{array} {c} a \\ c \\ y \end{array} \right)$. Итак, матричная форма записи заданной СЛАУ такова: $A\cdot X=B$. В развёрнутом виде:

$$ \left(\begin{array} {ccc} 4 & 0 & 3 \\ 2 & 7 & 4\\ -9 & 8 & 5 \\ 5 & -1 & 0 \end{array} \right) \cdot \left(\begin{array} {c} a \\ c \\ y \end{array} \right) = \left(\begin{array} {c} 17 \\ 10 \\ 25 \\ -4 \end{array} \right) $$

Расширенная матрица системы такова: $\left(\begin{array} {ccc|c} 4 & 0 & 3 & 17 \\ 2 & 7 & 4 & 10\\ -9 & 8 & 5 & 25 \\ 5 & -1 & 0 & -4 \end{array} \right) $.

Как видите, изменение порядка следования неизвестных равносильно перестановке столбцов матрицы системы. Но каким бы этот порядок расположения неизвестных ни был, он должен совпадать во всех уравнениях заданной СЛАУ.

Линейные уравнения

Линейные уравнения - относительно несложная математическая тема, довольно часто встречающаяся в заданиях по алгебре.

Системы линейных алгебраических уравнений: основные понятия, виды

Разберемся, что это такое, и как решаются линейные уравнения.

Как правило, линейное уравнение - это уравнение вида ax + c = 0, где а и с - произвольные числа, или коэффициенты, а х - неизвестное число.

К примеру, линейным уравнением будет:

Решение линейных уравнений.

Как решать линейные уравнения?

Решаются линейные уравнения совсем несложно. Для этого используются такой математический прием, как тождественное преобразование . Разберем, что это такое.

Пример линейного уравнения и его решение.

Пусть ax + c = 10, где а = 4, с = 2.

Таким образом, получаем уравнение 4х + 2 = 10.

Для того чтобы решить его было проще и быстрее, воспользуемся первым способом тождественного преобразования - то есть, перенесем все цифры в правую часть уравнения, а неизвестное 4х оставим в левой части.

Получится:

Таким образом, уравнение сводится к совсем простенькой задачке для начинающих. Остается лишь воспользоваться вторым способом тождественного преобразования - оставив в левой части уравнения х, перенести в правую часть цифры. Получим:

Проверка:

4х + 2 = 10, где х = 2.

Ответ верный.

График линейного уравнения.

При решении линейных уравнений с двумя переменными также часто используется метод построения графика. Дело в том, что уравнение вида ах + ву + с = 0, как правило, имеет много вариантов решения, ведь на место переменных подходит множество чисел, и во всех случаях уравнение остается верным.

Поэтому для облегчения задачи выстраивается график линейного уравнения.

Чтобы построить его, достаточно взять одну пару значений переменных - и, отметив их точками на плоскости координат, провести через них прямую. Все точки, находящиеся на этой прямой, и будут вариантами переменных в нашем уравнении.

Выражения, преобразование выражений

Порядок выполнения действий, правила, примеры.

Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :

действия выполняются по порядку слева направо,
причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Выполните действия 7−3+6.

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3, получаем 4, после чего к полученной разности 4 прибавляем 6, получаем 10.

Кратко решение можно записать так: 7−3+6=4+6=10.

Укажите порядок выполнения действий в выражении 6:2·8:3.

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

сначала 6 делим на 2, это частное умножаем на 8, наконец, полученный результат делим на 3.

Основные понятия. Системы линейных уравнений

Вычислите значение выражения 17−5·6:3−2+4:2.

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием.

Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6, получаем 30, это число делим на 3, получаем 10. Теперь 4 делим на 2, получаем 2. Подставляем в исходное выражение вместо 5·6:3 найденное значение 10, а вместо 4:2 — значение 2, имеем 17−5·6:3−2+4:2=17−10−2+2.

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7.

17−5·6:3−2+4:2=7.

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.

К началу страницы

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

К началу страницы

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Выполните указанные действия 5+(7−2·3)·(6−4):2.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1. Переходим ко второму выражению в скобках 6−4. Здесь лишь одно действие – вычитание, выполняем его 6−4=2.

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2.

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6.

5+(7−2·3)·(6−4):2=6.

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Выполните действия в выражении 4+(3+1+4·(2+3)).

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3).

Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5. Подставив найденное значение, получаем 3+1+4·5. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24. Исходное значение, после подстановки этого значения, принимает вид 4+24, и остается лишь закончить выполнение действий: 4+24=28.

4+(3+1+4·(2+3))=28.

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1. Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1, то после этого исходное выражение примет вид (4+(4+1)−1)−1. Опять выполняем действие во внутренних скобках, так как 4+1=5, то приходим к следующему выражению (4+5−1)−1. Опять выполняем действия в скобках: 4+5−1=8, при этом приходим к разности 8−1, которая равна 7.

К началу страницы

Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.

Рассмотрим решения примеров.

Выполните действия в выражении (3+1)·2+6 2:3−7.

В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36. Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7.

Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7=8+12−7=13.

(3+1)·2+6 2:3−7=13.

Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.

К началу страницы

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .

Математика : учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 21-е изд., стер. — М.: Мнемозина, 2007. — 280 с.: ил. ISBN 5-346-00699-0.

Запишите систему линейных алгебраических уравнений в общем виде

Что называется решением СЛАУ?

Решением системы уравнений называется набор из n чисел,

При подстановке которой в систему каждое уравнение обращается в тождество.

Какая система называется совместной (несовместной)?

Система уравнений называется совместной, если она имеет хотя бы одно решение.

Система называется несовместной, если она не имеет решений.

Какая система называется определенной (неопределенной)?

Совместная система называется определенной, если она имеет единственное решение.

Совместная система называется неопределенной, если она имеет больше одного решения.

Матричная форма записи системы уравнений

Ранг системы векторов

Ранг системы векторов называется максимальное число линейно независимых векторов.

Ранг матрицы и способы его нахождения

Ранг матрицы - наивысший из порядков миноров этой матрицы, определитель которых отличен от нуля.

Первый метод –- метод окантовки — заключается в следующем:

Если все миноры 1-го порядка, т.е. элементы матрицы равны нулю, то r=0 .

Если хоть один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю то r=1.

Если минор 2-го порядка отличен от нуля то исследуем миноры 3-го порядка. Таким образом находят минор k-го порядка и проверяют, не равны ли нулю миноры k+1-го порядка.

Если все миноры k+1-го порядка равны нулю, то ранг матрицы равен числу k. Такие миноры k+1-го порядка, как правило, находят путем "окантовки" минора k-го порядка.

Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при возведении ее к диагональному виду. Ранг такой матрицы равно числу отличных от нуля диагональных элементов.

Общее решение неоднородной системы линейных уравнений, его свойства.

Свойство 1. Сумма любого решения системы линейных уравнений и любого решения соответствующей однородной системы является решением системы линейных уравнений.

Свойство 2.

Системы линейных уравнений: основные понятия

Разность любых двух решений неоднородной системы линейных уравнений является решением соответствующей однородной системы.

Метод Гаусса решения СЛАУ

Последовательность:

1)составляется расширенная матрица системы уравнения

2)с помощью элементарных преобразований матрица приводится к ступенчатому виду

3)определяется ранг расширенной матрицы системы и ранг матрицы системы и устанавливается пакт совместимости или несовместимости системы

4)в случае совместимости записывается эквивалентная система уравнения

5)находится решение системы. Главные переменные выражаются через свободные

Теорема Кронекера-Капелли

Теоре́ма Кро́некера - Капе́лли - критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Для того чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы.

Когда система не имеет решения, когда имеет единственное решение, имеет множество решений?

Если число уравнений системы равно числу неизвестных переменных и определитель ее основной матрицы не равен нулю,значит Такие системы уравнений имеют единственное решение, причем в случае однородной системы все неизвестные переменные равны нулю.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

линейных уравнений называется совместной, если у неё есть хотя бы одно решение, и несовместной, если решений нет. В примере 14 система совместна, столбик является её решением:

Это решение можно записать и без матриц: x = 2, у = 1.

Систему уравнений будем называть неопределённой, если она имеет более одного решения, и определённой, если решение единственно.

Пример 15. Система является неопределённой. Например, … являются её решениями. Читатель может найти и много других решений этой системы.

Формулы, связывающие координаты векторов в старом и новом базисах

Научимся решать системы линейных уравнений сначала в частном случае. Систему уравнений AX = B будем называть крамеровской, если её основная матрица А - квадратная и невырожденная. Другими словами, в крамеровской системе число неизвестных совпадает с числом уравнений и |A| = 0.

Теорема 6 (правило Крамера). Крамеровская система линейных уравнений имеет единственное решение, задаваемое формулами:

где Δ = |A| - определитель основной матрицы, Δi - определитель, полученный из A заменой i-го столбика столбиком свободных членов.

Доказательство проведём для n = 3, так как в общем случае рассуждения аналогичны.

Итак, имеется крамеровская система:

Допустим сначала, что решение системы существует, т. е. имеются

Умножим первое. равенство на алгебраическое дополнение к элементу aii, второе равенство - на A2i, третье - на A3i и сложим полученные равенства:

Система линейных уравнений ~ Решение системы ~ Совместные и несовместные системы ~ Однородная система ~ Совместность однородной системы ~ Ранг матрицы системы ~ Условие нетривиальной совместности ~ Фундаментальная система решений. Общее решение ~ Исследование однородной системы

Рассмотрим систему m линейных алгебраических уравнений относительно n неизвестных
x 1 , x 2 , …, x n :

Решением системы называется совокупность n значений неизвестных

x 1 =x’ 1 , x 2 =x’ 2 , …, x n =x’ n ,

при подстановке которых все уравнения системы обращаются в тождества.

Система линейных уравнений может быть записана в матричном виде:

где A - матрица системы, b - правая часть, x - искомое решение, A p - расширенная матрица системы:

Система, имеющая хотя бы одно решение, называется совместной ; система, не имеющая ни одного решения - несовместной.

Однородной системой линейных уравненийназывается система, правая часть которой равна нулю:

Матричный вид однородной системы: Ax=0 .

Однородная система в с е г д а с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:

x 1 =0 , x 2 =0 , …, x n =0.

Если однородная система имеет единственное решение, то это единственное решение - нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.

Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно , чтобы определитель матрицы системы был равен нулю.

ПРИМЕР 1. Нетривиальная совместность однородной системы линейных уравнений с квадратной матрицей.

Применив к матрице системы алгоритм гауссова исключения, приведем матрицу системы к ступенчатому виду

Число r ненулевых строк в ступенчатой форме матрицы называется рангом матрицы, обозначаем
r=rg(A) или r=Rg(A).

Справедливо следующее утверждение.

Система линейных алгебраических уравнений

Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг r матрицы системы был меньше числа неизвестных n .

ПРИМЕР 2. Нетривиальная совместность однородной системы трех линейных уравнений с четырьмя неизестными.

Если однородная система нетривиально совместна, то она имеет бесконечное множество решений, причем линейная комбинация любых решений системы тоже является ее решением.
Доказано, что среди бесконечного множества решений однородной системы можно выделить ровно n-r линейно независимых решений.
Совокупность n-r линейно независимых решений однородной системы называется фундаментальной системой решений. Любое решение системы линейно выражается через фундаментальную систему. Таким образом, если ранг r матрицы A однородной линейной системы Ax=0 меньше числа неизвестных n и векторы
e 1 , e 2 , …, e n-r образуют ее фундаментальную систему решений (Ae i =0, i=1,2, …, n-r ), то любое решение x системы Ax=0 можно записать в виде

x=c 1 e 1 + c 2 e 2 + … + c n-r e n-r ,

где c 1 , c 2 , …, c n-r - произвольные постоянные. Записанное выражение называется общим решением однородной системы.

Исследовать

однородную систему - значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.

Исследуем однородную систему методом Гаусса.

матрица исследуемой однородной системы, ранг которой r< n .

Такая матрица приводится Гауссовым исключением к ступенчатому виду

Соответствующая эквивалентная система имеет вид

Отсюда легко получить выражения для переменных x 1 , x 2 , …, x r черезx r+1 , x r+2 , …, x n . Переменные
x 1 , x 2 , …, x r называют базисными переменными, а переменные x r+1 , x r+2 , …, x n - свободными переменными.

Перенеся свободные переменные в правую часть, получим формулы

которые определяют общее решение системы.

Положим последовательно значения свободных переменных равными

и вычислим соответствующие значения базисных переменных. Полученные n-r решений линейно независимы и, следовательно, образуют фундаментальную систему решений исследуемой однородной системы:

Исследование однородной системы на совместность методом Гаусса.

Системой m линейных уравнений с n неизвестными называется система вида

где a ij и b i (i =1,…,m ; b =1,…,n ) – некоторые известные числа, а x 1 ,…,x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы 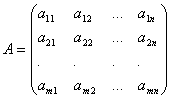, которую назовём матрицей системы .

Числа, стоящие в правых частях уравнений, b 1 ,…,b m называются свободными членами.

Совокупность n чисел c 1 ,…,c n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c 1 ,…,c n вместо соответствующих неизвестных x 1 ,…,x n .

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной . В противном случае, т.е. если система не имеет решений, то она называется несовместной .

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

Найдем произведение

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A ∙X=B .

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением .

Пусть определитель матрицы отличен от нуля |A | ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A : . Поскольку A -1 A = E и E ∙X = X , то получаем решение матричного уравнения в виде X = A -1 B .

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных . Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B .

Примеры. Решить системы уравнений.

ПРАВИЛО КРАМЕРА

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы .

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство . Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A 11 элемента a 11 , 2-ое уравнение – на A 21 и 3-е – на A 31 :

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x 1 . Для этого второе уравнение разделим на а 21 и умножим на –а 11 , а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а 31 и умножим на –а 11 , а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x 2 . Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x 3 , затем из 2-го уравнения x 2 и, наконец, из 1-го – x 1 .

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

перестановка строк или столбцов;
умножение строки на число, отличное от нуля;
прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Таким образом, система имеет бесконечное множество решений.

Система называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой , если она не имеет решений.

Определённая, неопределённая СЛАУ.

Если СЛАУ имеет решение и при том единственное, то её называют определённой а если решение неединственное – то неопределённой .

МАТРИЧНЫЕ УРАВНЕНИЯ

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

Найдем произведение

или короче A ∙X=B .

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Формулы Крамера

Метод Крамера состоит в том, что мы последовательно находим главный определитель системы , т.е. определитель матрицы А: D = det (a i j) и n вспомогательных определителей D i (i= ), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.

Формулы Крамера имеют вид: D × x i = D i (i = ).

Из этого следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам: x i = D i / D.

Если главный определитель системы D и все вспомогательные определители D i = 0 (i= ), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

Теорема (правило Крамера): Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство: Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A 11 элемента a 11 , 2-ое уравнение – на A 21 и 3-е – на A 31 :

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца .

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: . Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Теорема Кронекера - Капелли.

Система линейных уравнений является совместной тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы .

Доказательство: Оно распадается на два этапа.

1. Пусть система имеет решение. Покажем, что .

Пусть набор чисел является решением системы. Обозначим через -ый столбец матрицы , . Тогда , то есть столбец свободных членов является линейной комбинацией столбцов матрицы . Пусть . Предположим, что . Тогда по . Выберем в базисный минор . Он имеет порядок . Столбец свободных членов обязан проходить через этот минор, иначе он будет базисным минором матрицы . Столбец свободных членов в миноре является линейной комбинацией столбцов матрицы . В силу свойств определителя , где -- определитель, который получается из минора заменой столбца свободных членов на столбец . Если столбец проходил через минор M, то в , будет два одинаковых столбца и, следовательно, . Если столбец не проходил через минор , то будет отличаться от минора порядка r+1 матрицы только порядком столбцов. Так как , то . Таким образом, , что противоречит определению базисного минора. Значит, предположение, что , неверно.

2. Пусть . Покажем, что система имеет решение. Так как , то базисный минор матрицы является базисным минором матрицы . Пусть через минор проходят столбцы . Тогда по теореме о базисном миноре в матрице столбец свободных членов является линейной комбинацией указанных столбцов:

(1)

Положим , , , , остальные неизвестные возьмем равными нулю. Тогда при этих значениях получим

В силу равенства (1) . Последнее равенство означает, что набор чисел является решением системы. Существование решения доказано.

В рассмотренной выше системе , и система является совместной. В системе , , и система является несовместной.

Замечание:Хотя теорема Кронекера-Капелли дает возможность определить, является ли система совместной, применяется она довольно редко, в основном в теоретических исследованиях. Причина заключается в том, что вычисления, выполняемые при нахождении ранга матрицы, в основном совпадают с вычислениями при нахождении решения системы. Поэтому, обычно вместо того, чтобы находить и , ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.

Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)

Пусть дана система линейных уравнений с неизвестными . Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Метод, который будет изложен в этом разделе, близок к методу вычисления определителя и к методу нахождения ранга матрицы. Предлагаемый алгоритм называется методом Гаусса или методом последовательного исключения неизвестных.

Выпишем расширенную матрицу системы

Назовем элементарными операциями следующие действия с матрицами:

1. перестановка строк;

2. умножение строки на число, отличное от нуля;

3. сложение строки с другой строкой, умноженной на число.

Отметим, что при решении системы уравнений, в отличие от вычисления определителя и нахождения ранга, нельзя оперировать со столбцами. Если по матрице, полученной из выполнением элементарной операции, восстановить систему уравнений, то новая система будет равносильна исходной.

Цель алгоритма -- с помощью применения последовательности элементарных операций к матрице добиться, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.

Шаг алгоритма заключается в следующем. Находим первый ненулевой столбец в матрице . Пусть это будет столбец с номером . Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений, будем считать, что такая смена строк в матрице уже произведена, то есть . Тогда ко второй строке прибавим первую, умноженную на число , к третьей строке прибавим первую, умноженную на число , и т.д. В результате получим матрицу

(Первые нулевые столбцы, как правило, отсутствуют.)

Если в матрице встретилась строка с номером k, в которой все элементы равны нулю, а , то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что -ое уравнение будет иметь вид

Этому уравнению не удовлетворяет ни один набор чисел .

Матрицу можно записать в виде

По отношению к матрице выполняем описанный шаг алгоритма. Получаем матрицу

где , . Эту матрицу снова можно записать в виде

и к матрице снова применим описанный выше шаг алгоритма.

Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее.

Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида

Далее выполняется так называемый обратный ход метода Гаусса. По матрице составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть . Заметим, что . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части.

Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы Ax=b. Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами , включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин (в частности, просто произвольной величиной ). Эта запись и будет общим решением системы.

Если система была однородной, то получим общее решение однородной системы. Коэффициенты при , взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при -- второе решение и т.д.

Способ 2: Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одной переменной, перенесенной в правую часть, нужно присвоить значение 1, а остальным - нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другой переменной в правой части значение 1, а остальным - нули, получим второе решение из фундаментальной системы и т.д.

Определение:система называется совместно й, если она имеет хотя бы одно решение, и несовместной -- в противном случае, то есть в случае, когда решений у системы нет. Вопрос о том, имеет ли система решение или нет, связан не только с соотношением числа уравнений и числа неизвестных. Например, система из трех уравнений с двумя неизвестными

имеет решение , и даже имеет бесконечно много решений, а система из двух уравнений с тремя неизвестными.

……. … ……

A m 1 x 1 + … + a mn x n = 0

Данная система всегда совместна так как имеет тривиальное решение х 1 =…=х n =0

Для существования нетривиальных решений необходимо и достаточно выполнение

словия r = r(A) < n , что равносильно условию det(A)=0, когда матрица А – квадратная.

Th Совокупность решений СЛАУ образует линейное пространство размерности (n-r). Это означает, что произведение ее решения на число, а также сумма и линейная комбинация конечного числа ее решений является решениями этой системы. Линейное пространство решений любой СЛАУ является подпространством пространства R n .

Любая совокупность (n-r) линейно независимых решений СЛАУ (являющаяся базисом в пространстве решений) называется фундаментальной совокупностью решений(ФСР).

Пусть х 1 ,…,х r - базисные неизвестные, х r +1 ,…,х n – свободные неизвестные. Свободным переменным дадим поочередно следующие значения:

……. … ……

A m 1 x 1 + … + a mn x n = 0

Образует линейное пространство S (пространство решений), которое является подпространством в R n (n – число неизвестных), причем dims=k=n-r, где r- ранг системы. Базис в пространстве решений{x (1) ,…, x (k) } называется фундаментальной системой решений, и общее решение имеет вид :

X=c 1 x (1) + … + c k x (k) , c (1) ,…, c (k) ? R